Januray 1, 2020 to December 31, 2022
I am PI of this project. Project cost (200000 PLN) financed by IDUB PW.
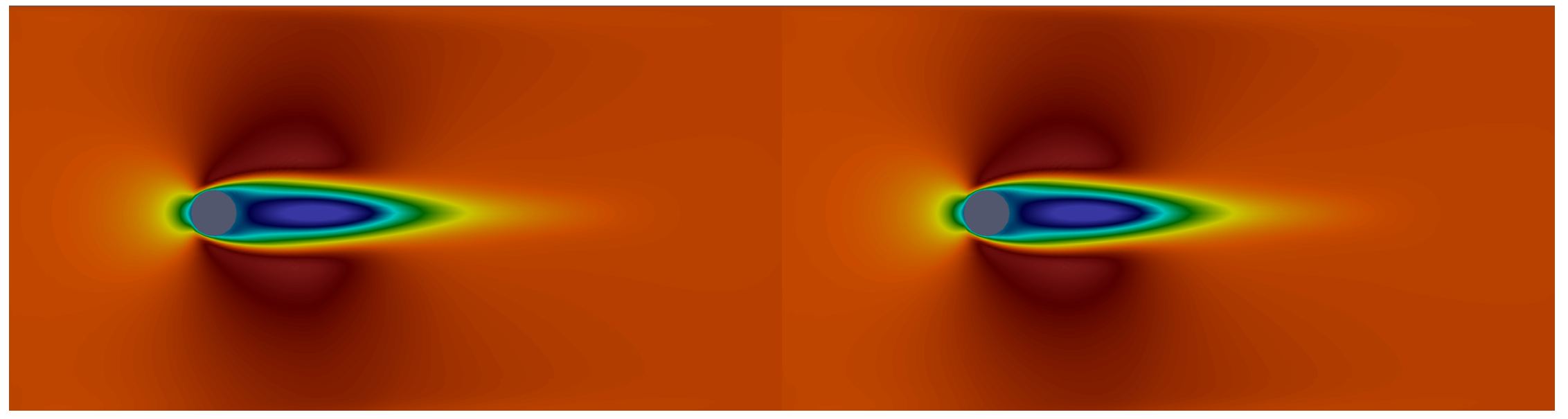
design of fluid mixers is a critical task in many industrial applications, including chemical engineering, food processing, and pharmaceuticals. One approach to optimizing the performance of fluid mixers is to use machine learning techniques to assist in the design process. In this particular case, we are interested in designing a laminar fluid mixer with spanwise actuation. The spanwise actuation refers to the introduction of a perpendicular flow component that can help in mixing the fluid in the transverse direction.
To start the design process, we used machine learning algorithms to create a model of the laminar fluid mixer's behavior. This model is trained on a dataset of known input and output parameters, such as the flow rate, fluid viscosity, and mixer geometry, and the resulting mixing efficiency.
Once we obtained a reliable model, we used it to explore the design space and optimize the mixer's performance. We can use techniques such as Bayesian optimization or genetic algorithms to search for the best combination of input parameters, such as the spanwise actuation frequency, the mixer blade angle, and the flow rate.
By using machine learning to assist in the design process, we can efficiently explore a vast design space and quickly identify optimal solutions. This approach can lead to the development of highly efficient fluid mixers that can be tailored to specific industrial applications.
Physics informed neural networks (PINNs) are a type of machine learning approach that combines the flexibility and accuracy of neural networks with the physical constraints of a system. PINNs have shown great potential in solving complex problems in various fields of physics, including fluid dynamics, solid mechanics, and electromagnetics. In the case of modeling acoustic waves, PINNs can be used to predict the propagation of sound waves in a given medium. The basic idea behind a PINN is to train a neural network to predict the behavior of the system while incorporating the governing equations of the system as a set of constraints during the training process. These governing equations can be derived from the fundamental principles of acoustics, such as the wave equation.
To use a PINN for acoustic wave modeling, we first defined the physical system and the corresponding equations that govern the propagation of sound waves. We then trained the neural network using input-output pairs, where the inputs represent the physical properties of the system (such as the density and speed of sound in the medium), and the outputs represent the predicted sound wave at a given time and location.
The neural network is trained to minimize the difference between the predicted wave and the actual wave, while also satisfying the governing equations of the system. This allows the neural network to learn the physics of the system and make accurate predictions even in cases where the data is incomplete or noisy.
Overall, PINNs provided a promising approach to modeling acoustic waves, and have the potential to be applied in a wide range of practical applications, such as noise reduction and acoustic imaging.
Feburary, 2019 to Januray, 2021
I am PI of this project. Project cost (100000 PLN) financed by NCN Poland.
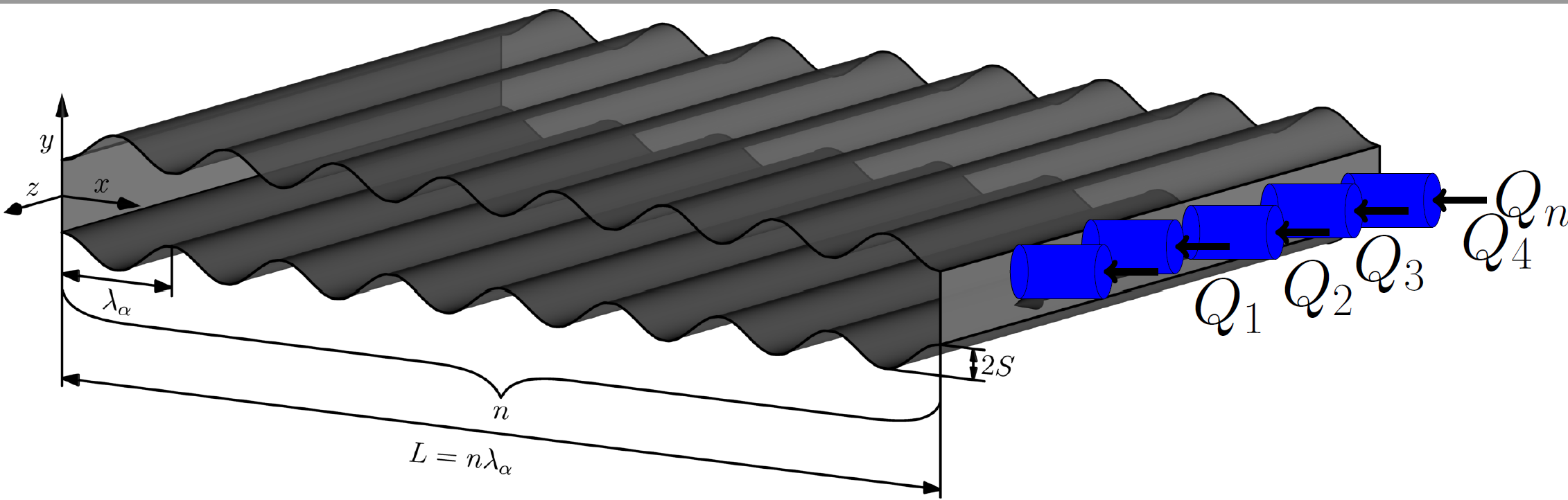
In the analysis of dynamic systems, stability is a crucial concept that refers to the system's behavior over time. A stable system will exhibit bounded behavior, meaning that its output will remain within a certain range of values, while an unstable system will exhibit unbounded behavior, meaning that its output will grow without bound.
Modal and non-modal stability analyses are two approaches to studying the stability of a dynamic system. Modal analysis focuses on the system's eigenvalues and eigenvectors, which describe the system's natural modes of oscillation. These modes represent the system's response to disturbances or inputs and can be used to determine whether the system is stable or unstable. A system is considered stable if all of its eigenvalues have negative real parts. Modal analysis is a linear technique, and its results depend on the initial conditions.
Non-modal stability analysis, on the other hand, considers the system's response to specific inputs or perturbations rather than its natural modes. This approach can be useful in studying the stability of non-linear systems or systems with time-varying parameters. Non-modal analysis can identify regions in the parameter space where the system is sensitive to perturbations and may become unstable.
Both modal and non-modal analysis techniques are essential tools in the analysis and design of dynamic systems. Modal analysis is useful for linear systems and provides insights into the system's natural behavior. Non-modal analysis, on the other hand, is useful for identifying specific inputs or disturbances that can cause instability in a system and can be used to design control strategies to stabilize the system.



